|
|
Post by Don Barone on May 23, 2020 11:56:45 GMT -5
Hi all I am going to present what I think is the solution to The Philosopher's Stone . A couple of clues led me to this analysis of this figure . The first was trying to incorporate The Sacred Code or Phi into the diagram and the second I am ashamed to say is that I kinda of cheated . I measured a nice clear image of this and by doing this realized that it was in the 6/5 ratio which I had encountered in many places in my studies . Here then is what could be the solution to The Philosopher's Stone


The solution I finally came up with was the result of many dead ends and erroneous solutions . I am including them along with my final diagram which I think is correct
|
|
|
|
Post by Don Barone on May 23, 2020 12:56:31 GMT -5
|
|
|
|
Post by Don Barone on May 23, 2020 13:07:32 GMT -5
This then is my final solution . A more detailed study is in one of several binders I have of my research . When I come across it, and I will, I will post it . 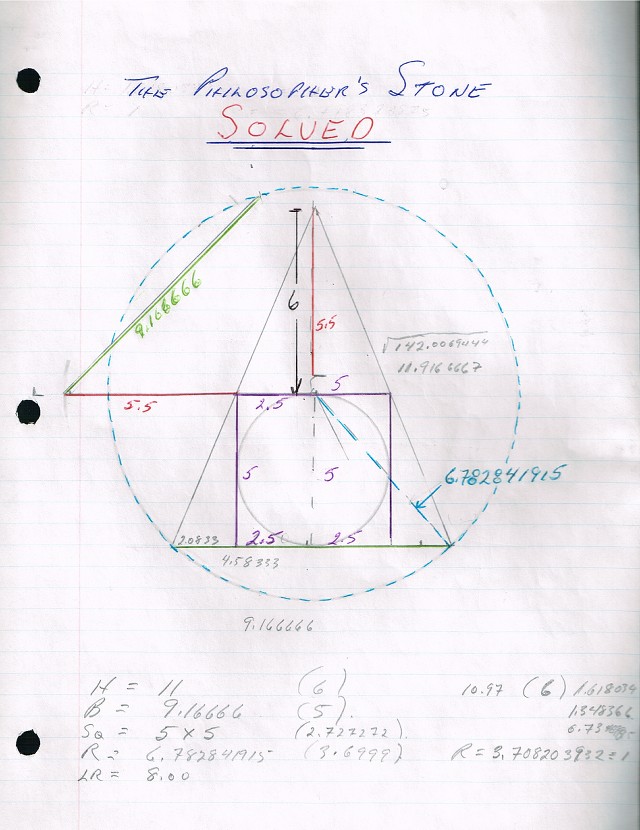 This is based on a 6/5 ratio as is the orbit of Mars,the ratio of Mercury's distance from the Sun and many other things . But the real key is that (5 x Pi) / 6 IS ALMOST EQUAL TO Phi squared or 2.618 The proof I think that The Pi world (or God) is never the same as The Phi World (or God) |
|
|
|
Post by Don Barone on Jun 8, 2020 21:02:07 GMT -5
Okay I had a nice long lead in but it disappeared so I am just going to say the solving of it came as a direct result of my studies of The Wood Pentagram and the numbers found there . 6 = 1.618033989 4.850421 = 1.236 (✓5 - 1) 3.7082 = 1 3 = 0.809016 AND realizing that the key numbers were 6 and 5 So I am going to build it on a blank image I have. Step 1 The Diagram as it first appeared: 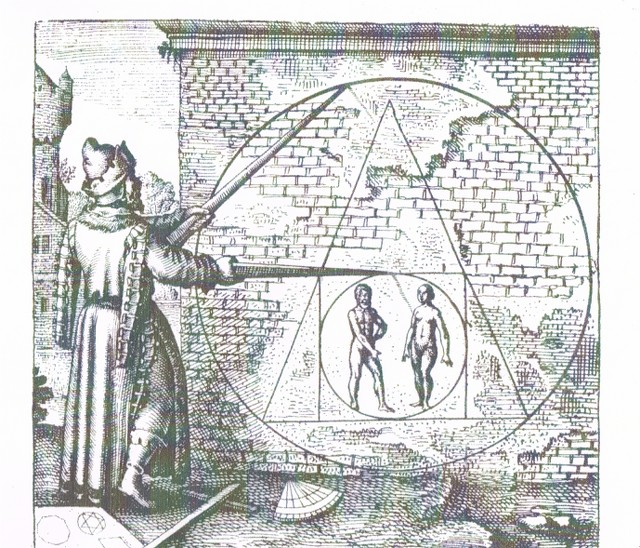 Step 2 Realizing that the bottom square is in the ration of 6 to 5  Solving for the known geometric figures. The small square and triangle.  All the measurements can be solved by simple trig. If in doubt ask The Strawman of Wizard of Oz fame. But the next little trick solves for Phi and reveals the hidden point that is behind his two hands 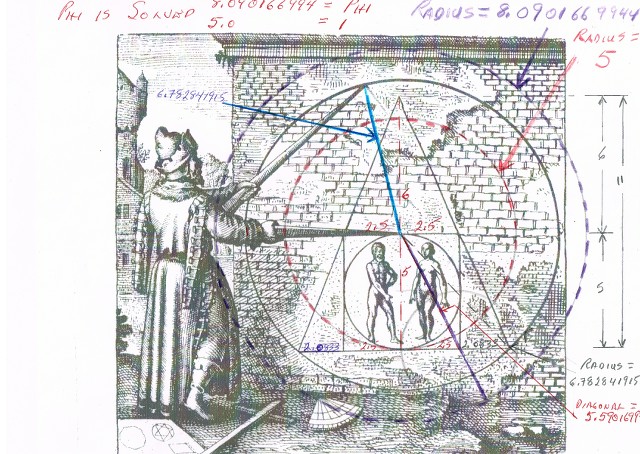 That solves for Phi but there is more to find More to |
|
|
|
Post by Don Barone on Jun 8, 2020 21:27:06 GMT -5
And then with the point where the top point of the compass is and compass distance set from that point scribe an arc and mark two points on the outer circle and then draw lines through the center and then join points  |
|
|
|
Post by Don Barone on Jun 8, 2020 21:40:27 GMT -5
And the final drawing .
It was only after solving it that I noticed he had placed the clues to the solution on the bottom left of the drawing
|
|
|
|
Post by Don Barone on Jun 8, 2020 21:46:45 GMT -5
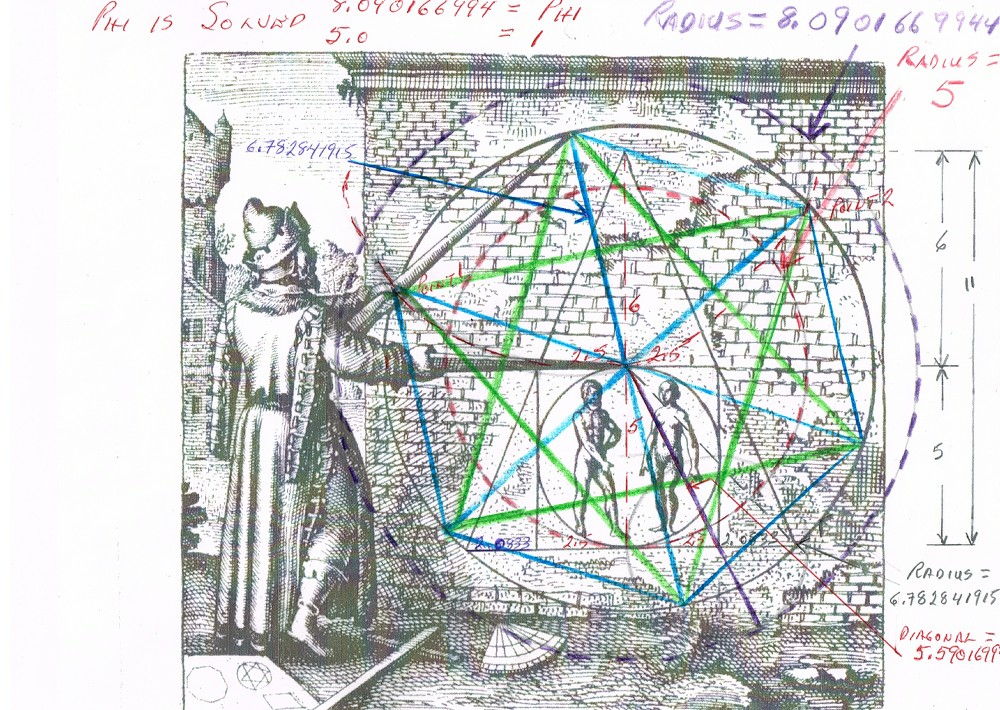
And my nice neat colorized version 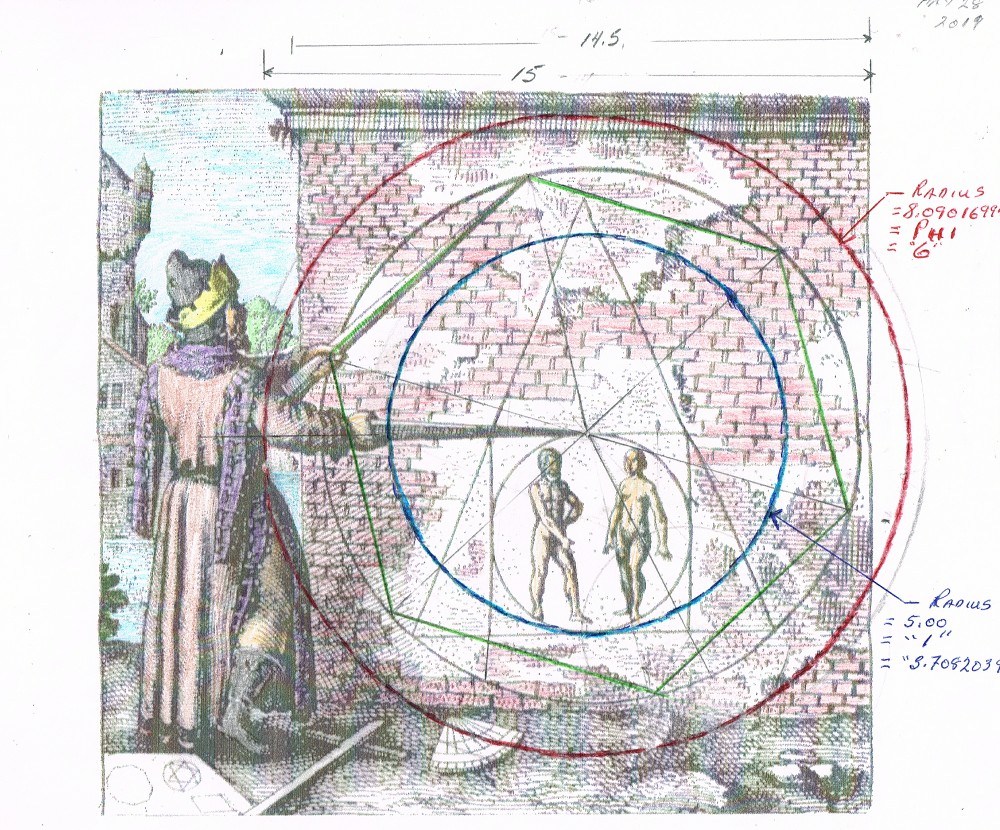 |
|
|
|
Post by Don Barone on Jun 8, 2020 22:02:42 GMT -5
And here are the instructions. See if you can now build your own  |
|
|
|
Post by Don Barone on Jun 9, 2020 11:38:45 GMT -5
Okay in the immortal words of Tom Hanks ... "Houston we have a problem"
After posting the last picture I went back and tried to build it as per the instructions . Drawing a circle and then the enclosing square of course was no problem but for the life of me I couldn't then and still can't now solve the dilemma of drawing the triangle . Only if you know it is in the 6/5 ratio can you solve it . I tried drawing just a random square and had no clue as to where to start the triangle . So here then is a clear picture of how it is solved but I still don't know how to establish the 6 distance
The image There was no way I could draw the compass angle at 45° and make it cross the 6.78 circle so that the chord made by the top arm of the compass equalled 6.78
|
|
|
|
Post by Don Barone on Jun 9, 2020 14:20:17 GMT -5
Well as Rex Harrison once said to My Fair Lady ... "By George I think he's got it"
The breakthrough came when I realized that you can not get 6 exactly in this diagram . The logical conclusion had to be ... that it was not 6 . But what was it ? Have a look at this diagram and realize that I measured nothing ! I simply drew a circle and then a square and used what was available to come up with this proper and final proof of the cracking of The Philosopher's Stone. The final proof for me was when I took the chord of the crossing compass and it divided the circle in precisely 6 equal chords .
Enjoy and feel free to share everywhere all I ask is that you give me credit, after all even "genius'" need their ego stroked 😎
The Final Drawing: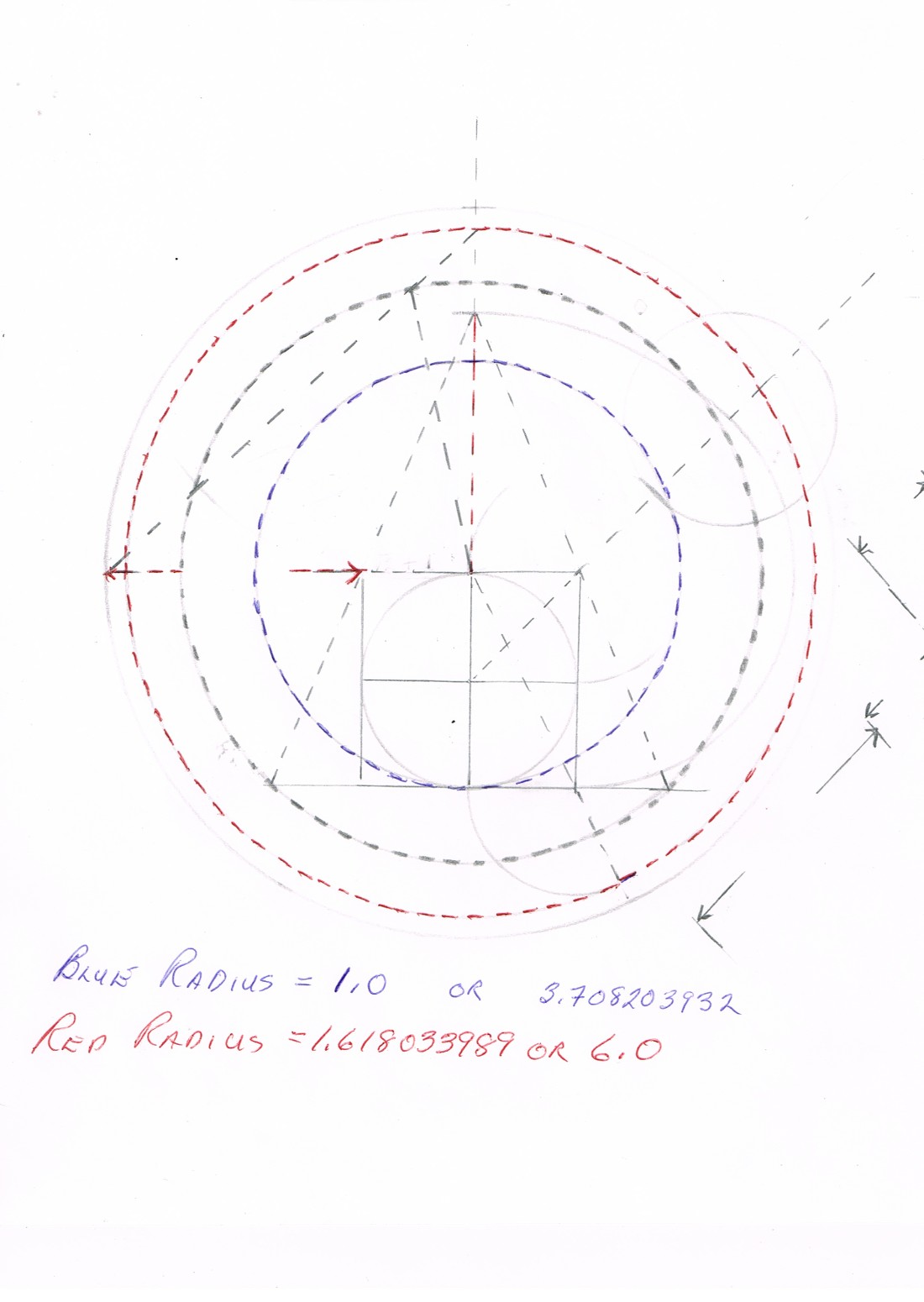 Amen
|
|
|
|
Post by Don Barone on Jun 11, 2020 13:19:00 GMT -5
Spoiler alert !!!
I have been thinking it was unfair to post that image so I am going to build it from scratch and using 5 as a random number chosen to supply numbers so you can see what's happening . I want to restate that I drew a random circle and then simply squared and here then is steps 1 and 2 (draw a circle then the square)
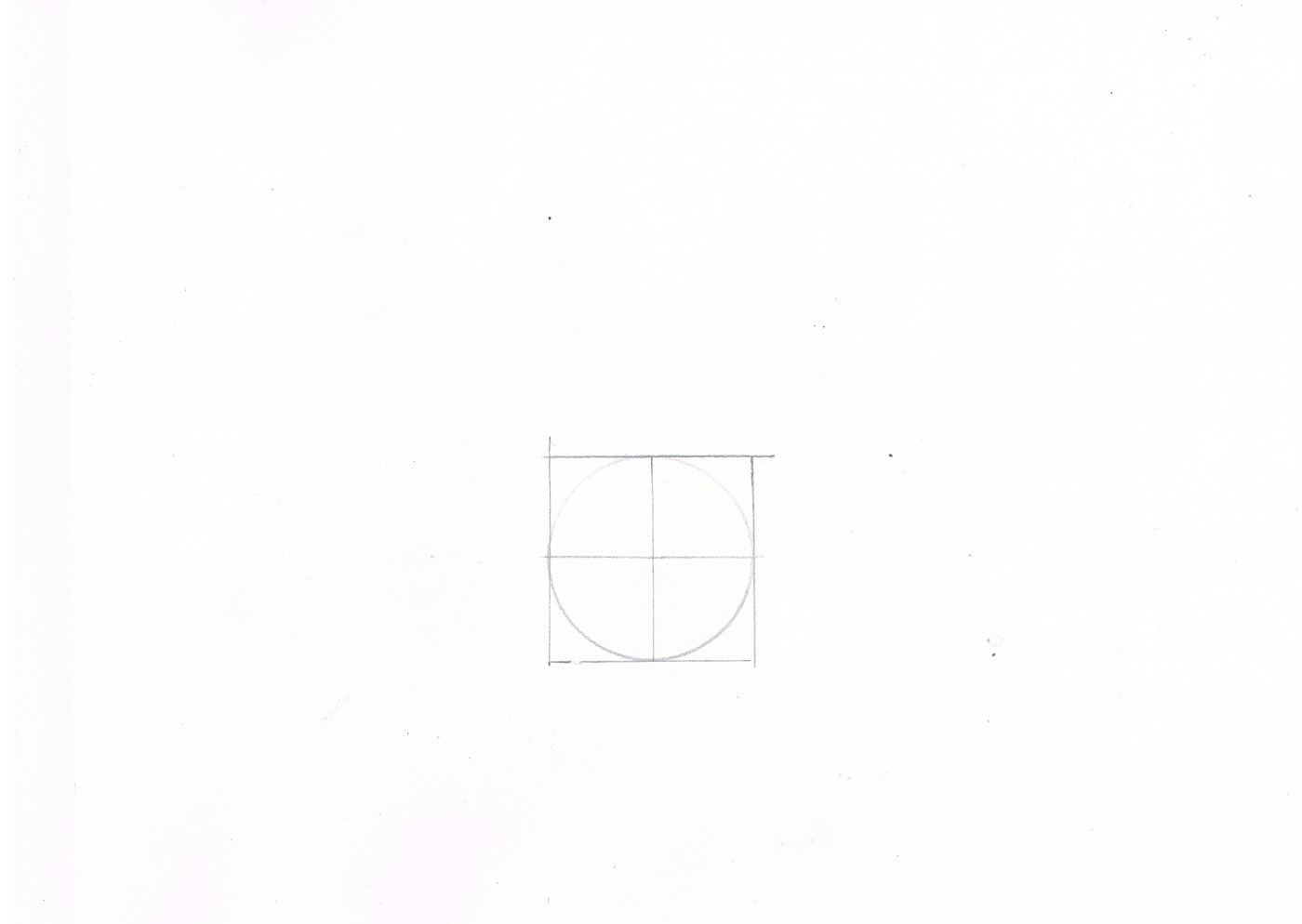
Okay the next step is the tricky one. It says draw the triangle but gives no clue how and how big it is . I scaled the diagram and assumed it was 6 but it wasn't . Here is the trick .
The diagonal of the quarter of the enclosing square yields ✓2 x 1/2 of half the square . I will use 5 because it is so much easier . Half 5 is 2.5 and the diagonal is ✓2.5 squared then times 2 or ✓12.5 or 3.53554
We then from the top right corner of the square and with radius of the diameter of the circle scribe an arc to cross the diagonal as shown in the next image and label "c'. Remember I am only assigning a number value to show you. This will work on any size circle and enclosing square
Step 3
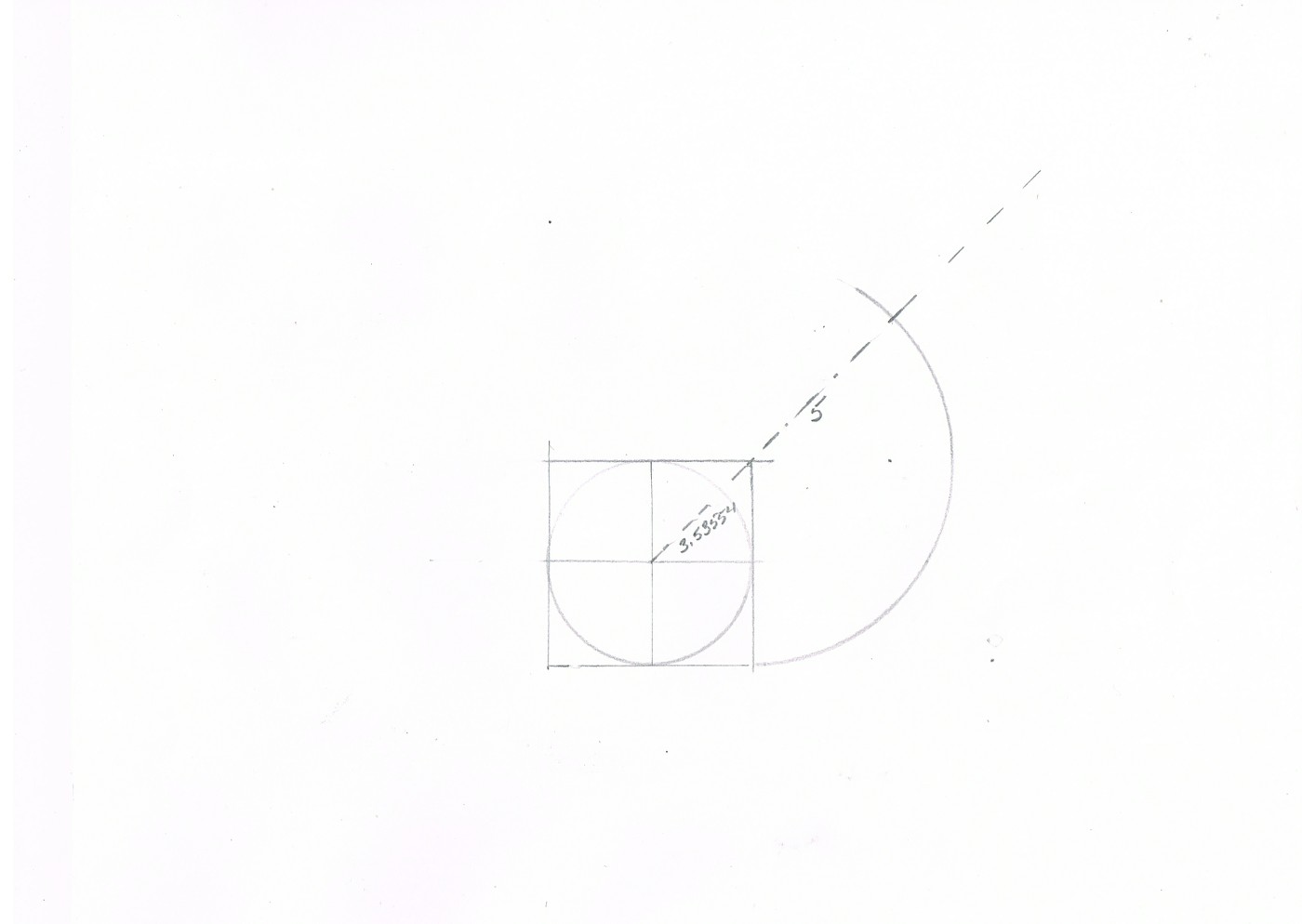
|
|
|
|
Post by Don Barone on Jun 11, 2020 13:31:14 GMT -5
Now with the center of our square and circle labelled "a" with distance ac draw a circle. Mark at 90° and call it "d" . Join this point and the top left and right of our square and extend down to extended base of square . Thus we have created the triangle of height of 3.53554 + 5 to get 8.53554 BUT we are measuring from the top of the square so we subtract 2.5 and we get ... 6.035533906 and NOT 6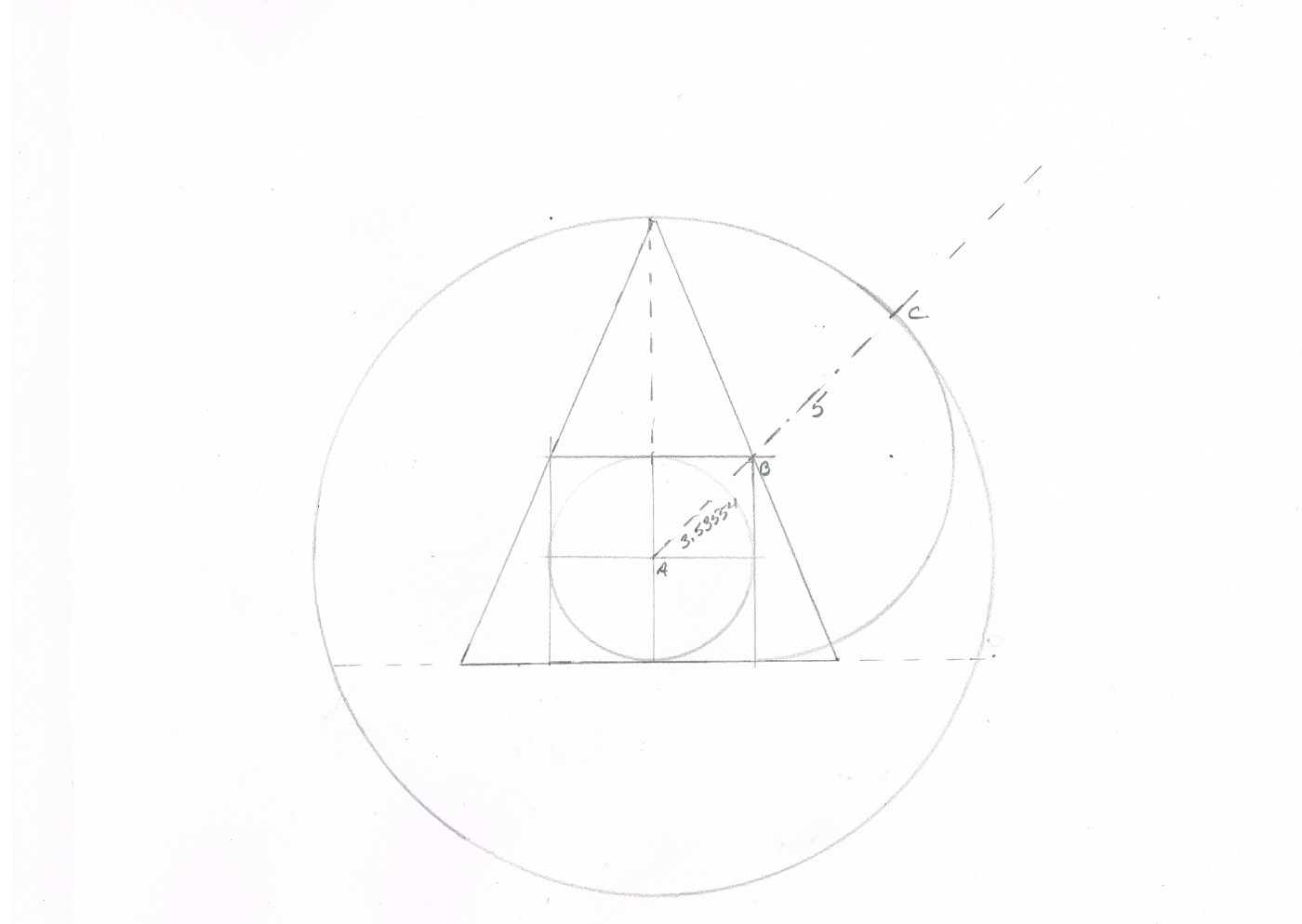
|
|
|
|
Post by Don Barone on Jun 11, 2020 14:26:00 GMT -5
Now in this next image we are going to find our Phi Ratio to our diameter and base of the square and we do this by joining d to f and extending it. We then with radius fe we scribe an arc to hit projection of df at h . Distance dh is ✓31.25 + 2.5 and equals 8.090169944
Note: 8.09169944 / 5 = 1.618034988 or Phi.
We then with radius dh we draw the circle and also draw circle with radius 5 while erasing unneeded circle of 8.53554 With radius dg draw another circle
Then from point "c" draw a circle of radius 2.5 to scribe extension of line ac at j . With radius now aj scribe an arc and mark point k on the center vertical . Now final circle with radius dk is drawn to get this image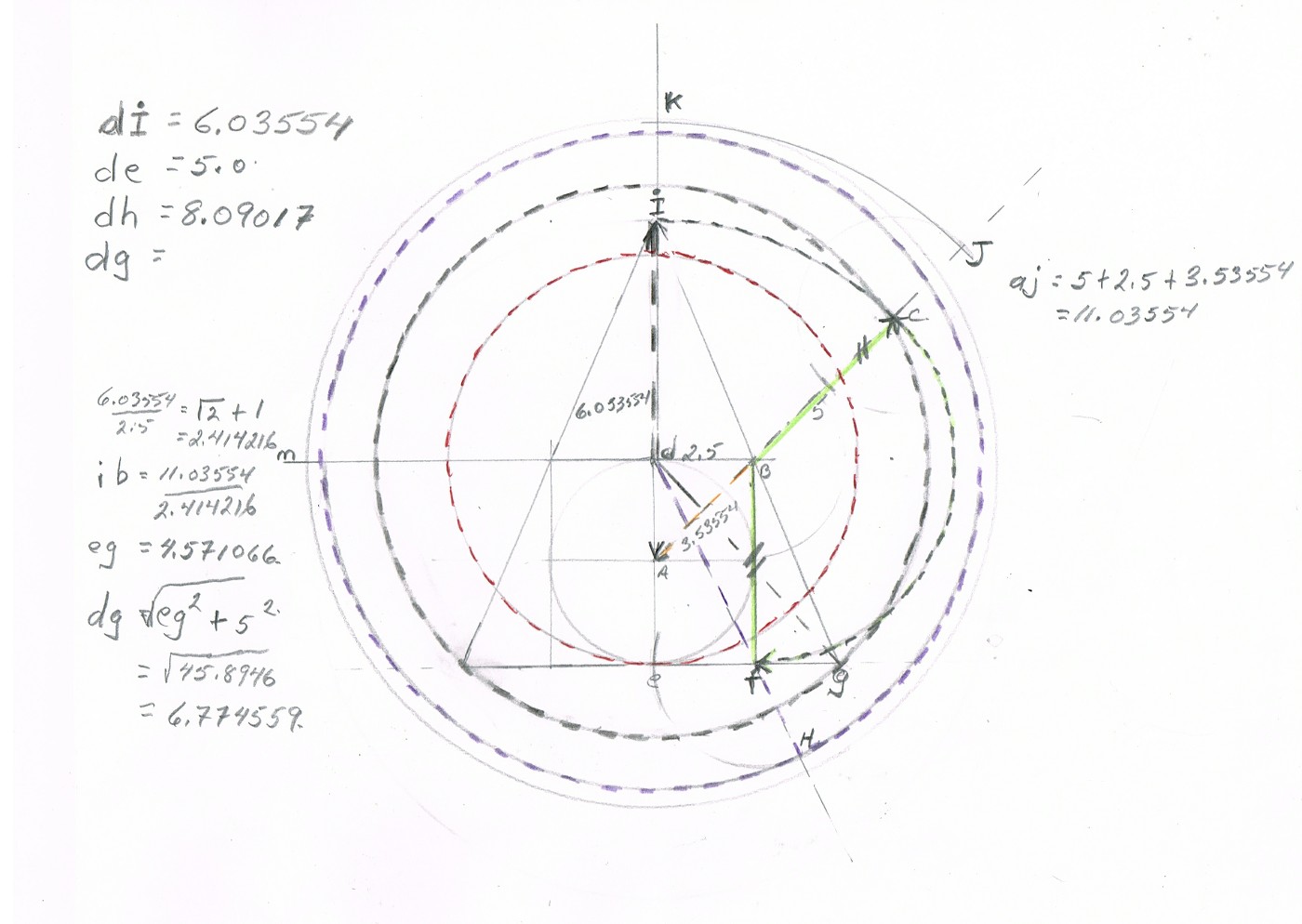
|
|
|
|
Post by Don Barone on Jun 11, 2020 14:40:18 GMT -5
Label point where 8.09 line crosses vertical as n
Join points m and n and where they cross 8.09 line label these p and q
Join d to p
dp now equals dq AND most importantly they also equal pq
dp = dq = pq
Philosopher's Stone or at least this version solved.
Of special note: in diagram the left hand is on point q and point m is hidden by his arms
This then is the final completed solution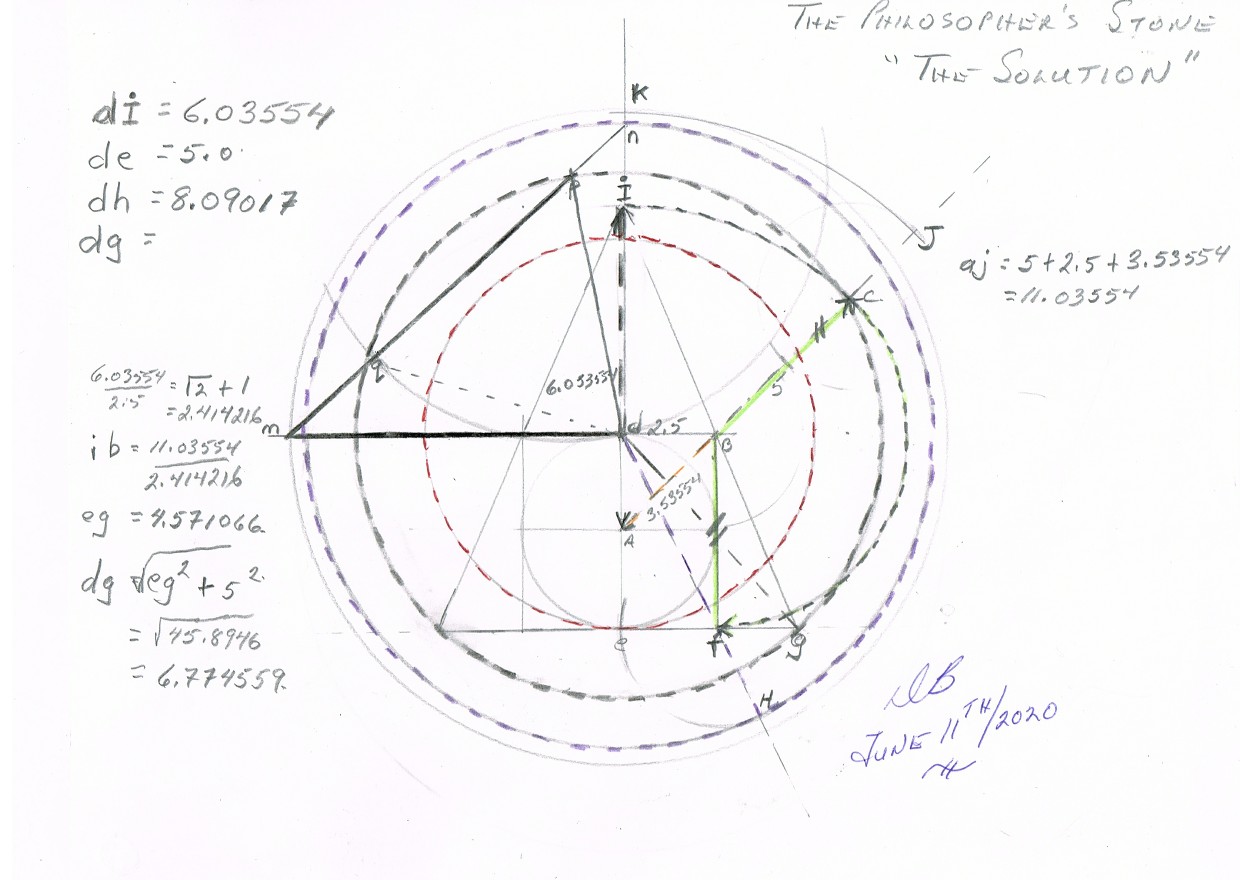
|
|
|
|
Post by Don Barone on Oct 20, 2023 23:23:50 GMT -5
A late image:
I decided to draw in the octagon because it was showing at the bottom of the page.
Octagon outside angles total 1080 - inside angles 360 = x's 3
Heptagon or Septagon outside angles total 900 - inside angles as always 360 = x's 2.5
Hexagon outside angles total 720 - inside angles again 360 = x's 2
Pentagon outside angle total 540 - inside angles again 5 x 72 and 360 = x's 1.5
Square outside angles total 360 - inside angles as always total 360 = x's 1.0
Triangle inside angle this time is 180 degrees = x's 0.5
Do you think maybe the inside angles always total 360 degrees ?
db
|
|
|
|
Post by Don Barone on Oct 29, 2023 9:35:18 GMT -5
Hi all I had noticed that my description of some of the early images were not as clear as I would have hoped so I have done them again. I hope this makes it much clearer and allows you to follow along with the brilliance of this design.
The first is simply the circle enclosed by a square. For demonstration purposes I have chosen 5 units as a length of the side and of course 5 units as the diameter of the circle.
Image 1
Image 2 and 3
In these next two image I have taken our point B and swung a radius of 5 units until it hits the line of our diagonal at a point I have labeled C . I have then shown that the smaller diagonal is the square root of 2.5 squared plus 2.5 squared and we get sq rt of 12.5 and this equals 3.535534 which is the sq rt of 2 divided by 4 then x 10
and
Image 4
In our next image I have our new larger diagonal labeled A to C or simply AC and swung an arc toward the vertical projection line from the centre of our square and labeled this point D as in the diagram below.
Image 5
In this image I have shown the two measurements involved in the vertical line and the distance from the top of the square labeled point E to our existing point D
Image 6 and the final image in this group. (There will be more coming)
In this image I draw the line down from point D and hitting the top corners and forming the triangle. There is a better and fuller explantaion on the diagram.
In the next posting I will add the other measurements that complete the image.
|
|
|
|
Post by Don Barone on Oct 29, 2023 13:01:24 GMT -5
Okay time to finish a bit more
Image 7
In this image I show you how the outside circle was established as well as what it's precise radius is.
Image 8
In the next image I am going to start to explain why I keep saying that this image shows us, not only the square root of 2 but now also found is the square root of three but we are going to start the process of finding Phi. First we need a new diagonal:
Image 9
With this image we are going to scribe another known arc onto it as seen below:
Image 10
In this image we get our new final diagonal and show the circle it draws:
and in Lucky 11 Image we finally find Phi ! No calculator, no tape measure, just compass, straightedge, and marker.
I am still working on geometrically marking the position of the compass on the circle and even though I know the angle of the compass is 45 degrees, and the angle from where it crosses the circle is 15 degrees and the remaining angles formed are 60 degrees I can't quite figure out how to prove it.
I am working on it even as we speak ...
db
|
|
|
|
Post by Don Barone on Oct 29, 2023 20:18:29 GMT -5
Hi all. I have an idea of certain things but at the moment the proof eludes me. An interesting observation I have made is that the line from the point of the compass vertically to the lower arc of the circle (drawn in green on the next two images) seems to be scaling to the same as the horizontal line as well and seem to be ( and this is just what I have scaled) the side of the square times The Silver Ratio of 2.614 (rnd). Thus any square times 2.614 or The Silver Ratio will give us this diagram. However I have yet to find the proof I need but it makes for an outstanding diagram and allows for the drawing of the 12 sided figure The Dodecagon
Here are the two images I have come up with.
Image 12
Showing the green lines and the red lines drawn through their intersections.
It is important to note here that the angle formed by the green lines is 15 degrees. So since there are two of them in any quadrant the remaining angle must be 60 degrees
More as I manage to find it.
db
|
|
|
|
Post by Don Barone on Oct 29, 2023 21:01:18 GMT -5
Okay here is my final image on this one for a while until I can prove what is in the picture below. I am pretty sure I am correct but I can't at the moment figure out how to draw the slope and Silver Ratio on this image. Hopefully it will come to me or maybe one of you can see the way for I am certain it is there.
Image 14
This is the solution but I am unsure how to get The Silver Ratio distance. I am, however, sure there is a solution.
Hope you have enjoyed this presentation
But wait there is just one more thing just discovered by me ...
The line from the origin to where the compass joins is really accurately 8.0656296487637652785664317342719 (sorry about the decimals but it is necessary to prove the next point.) This, if we made it a radius would give us a diameter of 2 x 8.0656296487637652785664317342719 or 16.131259297527530557132863468544. Please note again that The Silver Ratio is 2.6131259297527530557132863468544
Thus we have the final and largest diameter of a circle in this diagram equaling 10 times The Silver Ratio then minus 10.
10 x 2.6131259297527530557132863468544 = 26.131259297527530557132863468544 - 10 = 16.131259297527530557132863468544
THIS IS EXACTLY, AND I MEAN PRECISELY THE DIAMETER OF THIS CIRCLE OF 16.131259297527530557132863468544
db October 29th, 2023
|
|